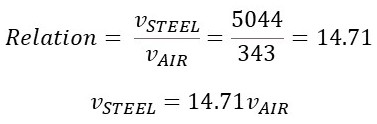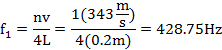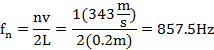Topic 5. Sound
|
Introduction:
Figure 5.1 shows the picture of a bell; it has the purpose of making sound of a good intensity. You can distinguish its sound from others because of its characteristic tone. While the bell can vibrate at a frequency (harmonics) equal to other instruments, it still can be distinguished.
Sound, besides of its frequencies and intensities, has other characteristics that you will study in this topic. By the end of the topic, you will know about sound’s propagation speed in different means (air, metal and water), its intensity and the effect when sound sources and listeners move.
Explanation:
5.1 Sound Speed
In the previous topic we studied the speed of transverse waves. For this topic we will focus on the speed of longitudinal waves.
Sound is a longitudinal wave because the vibrating molecules move in the same direction of the wave. In other words, a sound source emits a collection of air molecules, compressions and rarefactions that travel in the same direction of sound (see Figure 5.2).
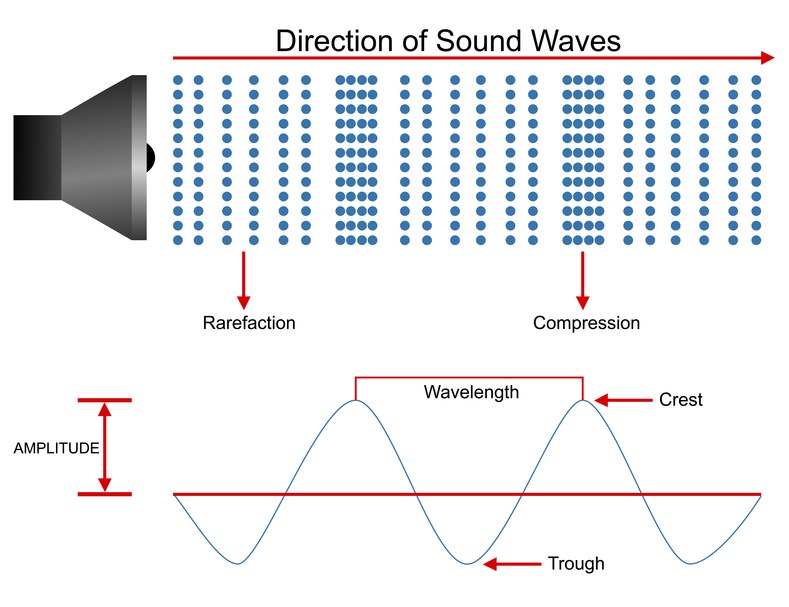
Figure 5.1 Sound Wave
We learned that the speed of a transverse wave is composed of a restoring force (tension force, FT) and an inertia factor (lineal density, µ). Similarly, a longitudinal wave will be composed of those factors that will vary according to the source and medium of propagation. For instance, the speed of sound in air is 343 m/s at room temperature, but in every other medium you need to use an equation to calculate it.
Here are the formulas to calculate the speed of sound’s propagation of different objects and mediums.
Speed of sound in a fluid
When the sound source is compressing a fluid, it’s important to take into consideration how difficult it is to compress the fluid (bulk modulus) and the inertia of the fluid (density). Thus, the formula for the propagation speed of sound is the following:
![]() (5.1)
(5.1)
Where:
B= bulk modulus
ρ= density of the fluid
Speed of sound in a metallic rod
When the sound source is compressing the molecules of a metallic rod, the elasticity (young modulus) and density of the metal are taken into consideration. The speed of propagation is then calculated by the following:
![]() (5.2)
(5.2)
Where:
Y= young modulus
ρ= density of the metal
Speed of sound in an gas
When sound is propagating in a gas medium, then the adiabatic constant (ϒ) and the pressure (P) of the gas work act as the restoring force. Therefore, the density of the gas (ρ) will act as the inertia factor. The formula for the speed of sound wave is the following:
![]() (5.3)
(5.3)
To calculate the speed in an ideal fluid, we can use the following equation:
![]() (5.4)
(5.4)
Where:
ϒ= adiabatic constant (1.4)
R= gas constant ![]()
T= gas temperature in kelvin
M= molecular mass of the gas
Speed of sound in an extended solid
To calculate the speed of sound traveling in an extended solid, we can use the next equation:
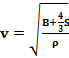 (5.5)
(5.5)
Where:
B= bulk modulus of the medium
S= shear modulus
Ρ= density of the material
Table 5.1 shows the different elasticity modulus for common materials.
Substance |
Young Modulus (Y) |
Shear Modulus (S) |
Bulk Modulus (B) |
Water |
-- |
-- |
0.21x1010 |
Steel |
20x1010 |
8.4x1010 |
6x1010 |
Copper |
11x1010 |
4.2x1010 |
14x1010 |
Brass |
9.1x1010 |
3.5x1010 |
6.1x1010 |
Mercury |
-- |
-- |
2.8x1010 |
Aluminum |
6.89x1010 |
2.5x1010 |
7x1010 |
Glass |
7.8x1010 |
3.2x1010 |
5.5x1010 |
Tungsten |
35x1010 |
14x1010 |
20x1010 |
Table 5.1 Elasticity Modulus in Pa
To review an example, click here.
5.2 Sound characteristics
Standing waves in a cylinder
In topic 4 we studied the harmonics of standing waves and considered a wave propagating on a string. According to the previous topic, we can say that for string instruments, the frequency depends on the mass of the string, its length and tension force.
Now we are going to analyze the harmonics in a tube. An example of this is a wind instrument like a trumpet, a flute, an organ, etc. For wind instruments, the frequency depends on the internal dimensions of the tube, its length and if it is an open or a closed tube.
An open tube is when the ends of a pipe are open (like in a flute). As the air passes through the tube, the compressions and rarefactions of the sound waves form resonant frequencies (series of nodes and antinodes).
The possible wavelengths on an open tube are calculated by using the following equation:
![]() (5.6)
(5.6)
Where:
n= starts from n=1 (one node) and increases by one (n= 1,2,3…)
L= length of the open tube
Since the speed of a wave (v) is calculated by ![]() , then solving for the frequency (f ) and using equation 5.6. The formula to calculate the harmonics of an open tube is the following:
, then solving for the frequency (f ) and using equation 5.6. The formula to calculate the harmonics of an open tube is the following:
![]() (5.7)
(5.7)
The values for n are n=1 (fundamental frequency) and increases by one.
In a closed tube the wavelengths and frequencies are going to be different. There will be one node and one antinode at the beginning and the end of the tube. Thus, the wavelength and frequency will be only odd numbers of n. The formula to calculate the wavelength of a sound wave in a closed tube is:
![]() (5.8)
(5.8)
Where n will be only odd numbers (n = 1,3,5…) and L is the length of the tube.
As the wavelength changed so is going to be the formula to calculate the harmonics on a closed tube. The formula is then given by the following:
![]() (5.9)
(5.9)
Again, the values for n will be only odd numbers, where n=1 represents the fundamental frequency, n=3 is the third harmonic and so on.
To review an example, click here.
Sound Intensity
So far, we have learned about the speed of propagation of sound and its frequency. But how is that related to hearing? Our ears can get the vibrations in the air and pass the information from our ears through our nervous system to the brain. Once it gets to the brain, the signal is transformed in what we know as sound.
Depending on the properties of sound, like frequency and intensity, is the kind of sound we will hear. The frequency of sound that a human can hear is a range from 20 Hz to 20 KHz.
Frequencies lower than 20 Hz are infrasonic waves and bigger than 20 KHz are ultrasonic waves.
The sound intensity is another important property because is what we know as volume. The louder a sound is, the bigger the intensity of the wave.
The intensity of sound is the energy at which sound propagates. Sound intensity is related to the power per unit area of the wave. The formula to calculate it, is the following:
![]() (5.10)
(5.10)
Where:
I= sound intensity (W/m2)
P= power (W)
A= cross sectional area of the wave (m2)
The minimum intensity for human hearing at 1000 Hz is:
![]()
The maximum intensity for human hearing is:
![]()
Above this intensity, there will be a sensation of pain inside the ear.
The Bel scale
The intensity of sound is usually measured in bels (B). The Bel scale is used to compare intensities of two sounds (I1 and I2).
![]() (5.11)
(5.11)
Since the bel is a large scale, you will see often the intensity in decibels (dB). The decibel scale compares the intensity of a sound (I) with the intensity of the minimum intensity for human hearing (I0).
![]() (5.12)
(5.12)
To review an example, click here.
5.3 Doppler Effect
A very interesting phenomenon related to sound is the Doppler Effect. This effect is the reason why you hear an approaching ambulance at a high pitch and once it passes you, you hear a low pitch.
Tippens (2011) states that the Doppler Effect refers to the apparent change in the frequency of a sound source when there is a relative movement of the source regarding to the listener. In other words, it’s the change in frequency that a person will hear if the person or the sound source moves.
Figure 5.2 shows this effect. If you were standing in front of the police car, the sound waves would be getting closer together and you would hear a high pitch. Once it passes by, you will hear a low pitch because sound waves will be getting further apart. If there were no motion from you or the police car, you would hear the same pitch in the front and back.
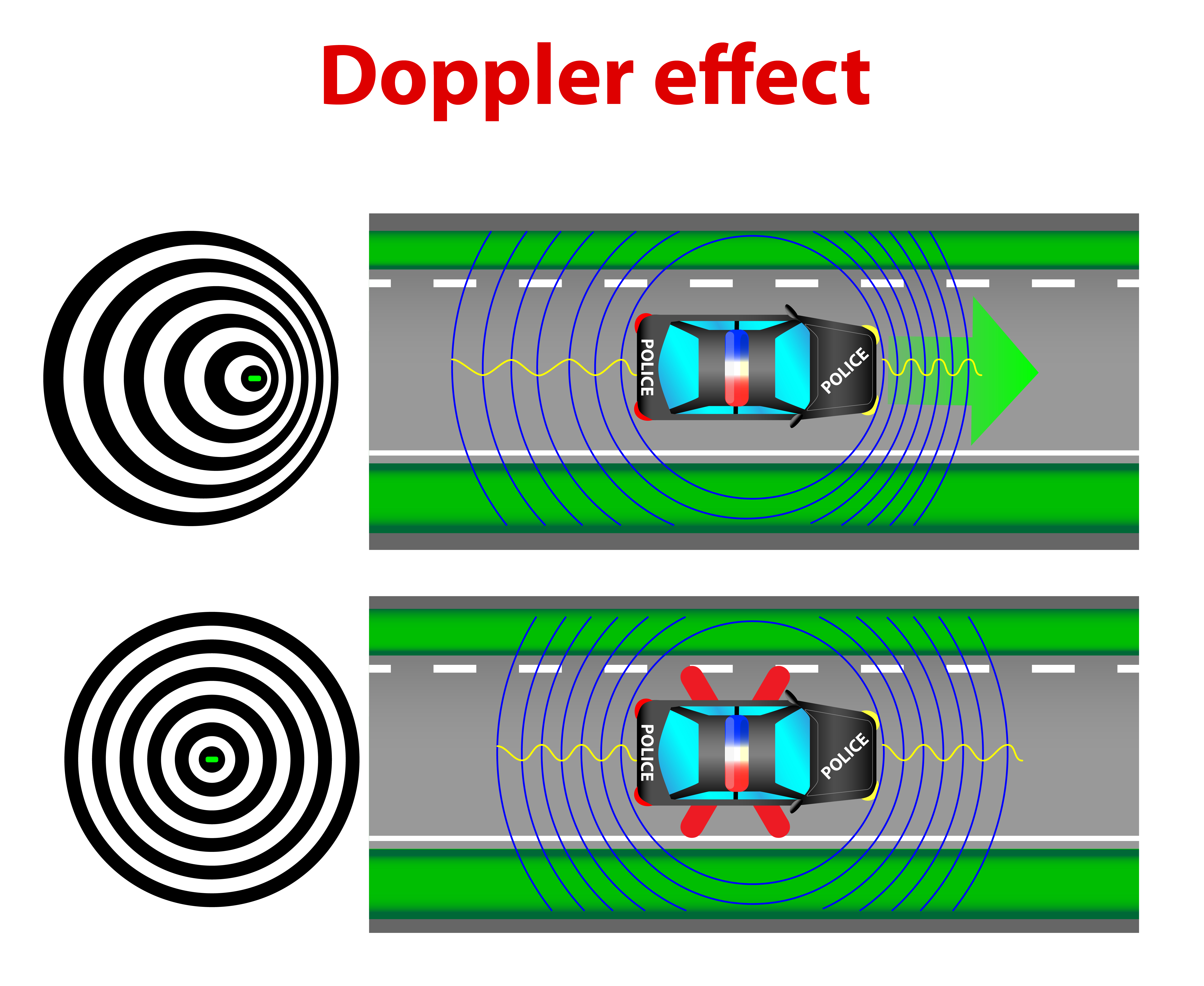
Figure 5.2 Doppler Effect
To calculate the sound frequency, we need to take into consideration if the source, the listener or both are moving.
Moving Source
To calculate the sound frequency heard by a listener if the source is moving, we need to use the following equation:
![]() (5.13)
(5.13)
Where:
fL= frequency heard by the listener (Hz)
V= speed of propagation of sound (343m/s in air at room temperature)
vs= speed of the source (m/s)
fs= frequency emitted by the source (Hz)
The positive sign (+) is used when the source is moving away from the listener and the negative sign (-) when the source is approaching the listener.
Moving Observer
If the observer is the one approaching or leaving a sound source, then the mathematical equation is the following:
![]() (5.14)
(5.14)
Where:
fL= frequency heard by the listener (Hz)
V= speed of sound (343m/s in air at room temperature)
vL= speed of the listener (m/s)
fs= frequency emitted by the source (Hz)
The positive sign (+) is used when the listener is approaching the source and the negative sign (-) when the listener is moving away from the source.
Moving Source and Observer
If both the listener and the source are moving, the equation is the following:
![]() (5.15)
(5.15)
Where:
fL= frequency heard by the listener (Hz)
V= speed of sound (343m/s in air at room temperature)
vL= speed of the listener (m/s)
vs= speed of the source (m/s)
fs= frequency emitted by the source (Hz)
The positive sign (+) is used when the listener is approaching the source and the negative sign (-) when the listener is moving away from the source (numerator).
The positive sign (+) is used when the source is moving away from the listener and the negative sign (-) when the source is approaching the listener (denominator).
Click here to see an example of the Doppler Effect.
Closure:
Hearing will not be the same!
In this topic you learned several sound properties; this way, when hearing a sound you will go beyond perception and detect all its characteristics.
Bibliographic references:
- Tippens, P. (2011). Física: Conceptos y aplicaciones (7th Ed.). México: McGraw-Hill.

Checkpoint
Make sure you understand:
- The speed of sound in different mediums.
- The characteristics of sound: frequency and intensity.
- The Doppler Effects and the situations that may be present between an observer and a source.