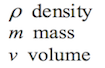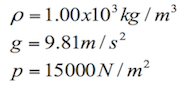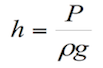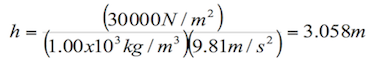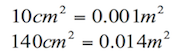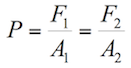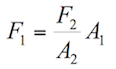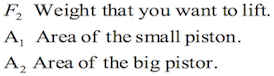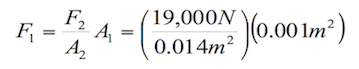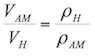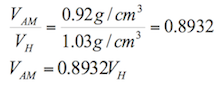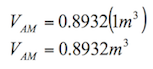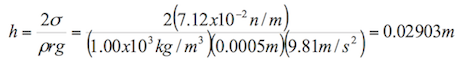Topic 1. Fluids at rest

Introduction:

A fluid is often defined as a matter that has the ability to flow. For example, water coming out of a faucet or cool air traveling through air ducts.

For this topic we are going to analyze physical principles related to fluids at rest. Pascal’s principle, Archimedes’ principle, surface tension and capillarity are some examples of the principles you are going to be able to understand.

Once you finish this topic, analyze Figure 1.1 and explain it in terms of the physical principles you learned.

Figure 1.1 Fluid at rest

---

Explanation:

1.1 Pressure and Pascal's principle

Density

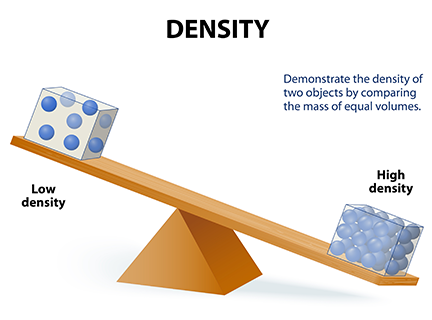
To study pressure, it is necessary to know the concept of density first. Density is the amount of matter per unit volume. In other words, density is the amount of atoms or molecules in a definite space. For instance, a gallon full of milk will be heavier than a gallon full of air. The explanation for this is that air is less dense than milk, thus there are more milk molecules than air molecules in the same volume (see Figure 1.2). Mathematically speaking, density can be obtained by the following formula:

 

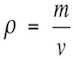     (1.1)

Where:

Figure 1.2 Densities of different materials

Materials have different densities; the following table includes some of them:

Table 1.1 Densities of some common substances.
Source: Sears, F. y Zemansky, M. (2013). Física universitaria con física moderna (13th Ed.). México: Pearson.

Click on each example to know the information.

Pressure

When someone shakes your hand, you feel pressure on it. Then, what is pressure? In physics, pressure is the force applied on a surface. Thus, the pressure you feel during a handshake is the force applied by the other hand on the surface of your hand.

Fluids exert pressure on objects immersed in them, a fluid also applies pressure on the walls of a container. For example, when you dive in a swimming pool, water exerts pressure on your body. Similarly, butane gas exerts pressure on a gas tank.

The mathematical expression for pressure is the following:

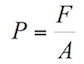     (1.2)

Where:

The SI unit of pressure is Pascal (Pa), which has the following equivalence:

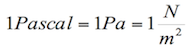
Pressure and height

The amount of pressure an incompressible fluid or a liquid exerts on a body also depends on its density and depth. For example, we can think of the pressure a diver feels when is descending in the ocean. The deeper the diver goes, the more the pressure on the body.

The formula for pressure in terms of density and depth is the following:

            (1.3)

Where:

P= pressure
g= gravity (9.81 m/s2)
h= height

Equation 1.3 can also be expressed in terms of the specific weight (D) or weight per unit volume of the fluid. The formula for specific weight is the following:

                (1.4)

Thus, the pressure formula in terms of specific weight is given by:

                (1.5)

Atmospheric pressure

On the surface of this planet, the air mass of the atmosphere applies pressure that changes with depth. This kind of pressure is known as atmospheric pressure. Atmospheric pressure changes with the altitude, time and weather conditions. Generally, bodies at sea level  experience a pressure equivalent to one atmosphere, and it has the following equivalence in Pascals:

Pascal’s Principle

In 1653, the scientist Blaise Pascal discovered that incompressible fluids transmit the same amount of pressure through all of the fluid if a force is applied at any point. He proposed a law called Pascal’s principle

Pascal's Principle states that “Pressure applied to an enclosed fluid is transmitted undiminished to every part of the fluid, as well as to the walls of the container” (Sears & Zemansky, 2013).

This law has its principal application in the hydraulic lift, because it obtains different forces (F1 and F2) by applying the same pressure in different areas (A1 and A2). The following figure shows the hydraulic lift functioning:

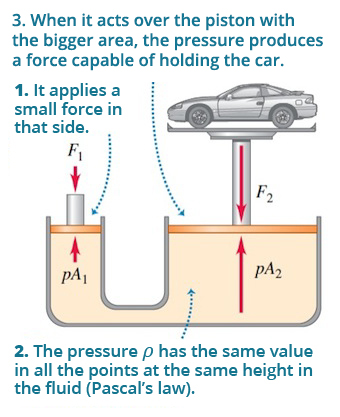
Figure 1.2 The hydraulic elevator.
Source: Sears, F. y Zemansky, M. (2013). Física universitaria con física moderna (13th ed.). México: Pearson/ Addison-Wesley.

Applying the Pascal principle in figure 1.2, it can be stated that:

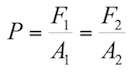     (1.6)

Where:

F1= Force applied on the smaller piston
A1= Area of the smaller piston
F2= Force applied by the fluid on the second piston
A2= Area of the second piston

In the following subtopic you will know another principle applicable to fluids at rest.

---

1.2 Flotation and Archimedes principle

 

When a body immersed in a fluid is less dense than the fluid, it will float. For example, a hot air balloon will float because heating the air will make the air molecules to gain energy and scatter away.

Hot air is less dense than cool air which will cause the balloon to be buoyant. Flotation is caused by an upward force called buoyant force.

Archimedes’ principle states: “The buoyant force on an object immersed in a fluid is equal to the weight of the fluid displaced by that object.”(Giancoli, 2005)

Archimedes’ principle explains the reason why metallic ships float. Although metal is denser than water, the distribution of the metal will make that the weight of the displaced water be the same as the weight of the ship. Thus, the buoyant force will be the same as the ship’s weight and will make it float.

In other words, if we weight the ship and then the water displaced by it, we will see that is the same value. This is the condition for buoyancy: if the buoyant force is equal or bigger than the weight of the object it will float, otherwise it will sink.

Observe figure 1.4 and explain why the first two materials float and the third one sinks.

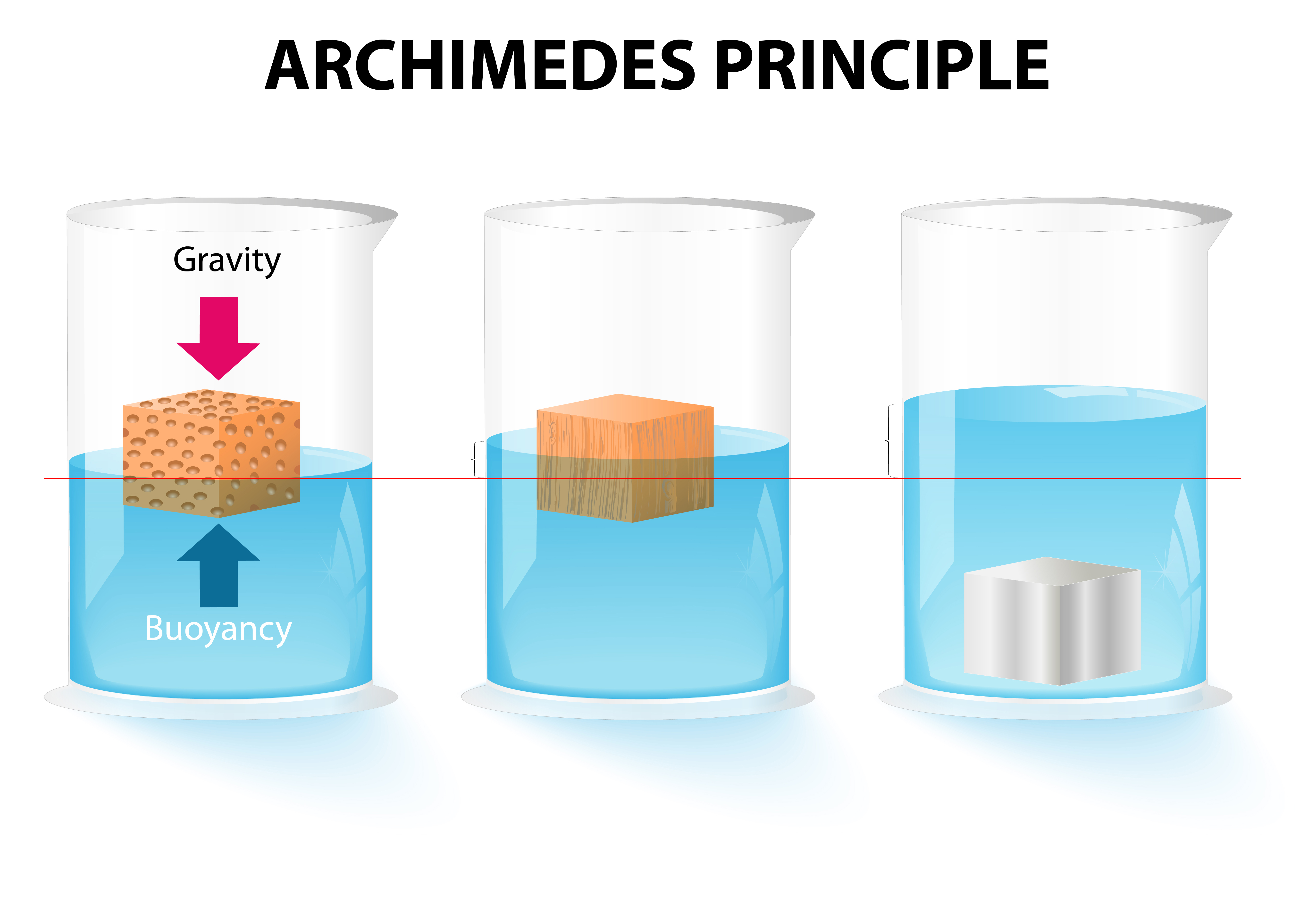
Figure 1.4 Archimedes' principle

The buoyant force can be calculated by the following formula:     

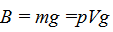(1.7)

Where:

 

 

 

---

1.3 Superficial tension and capillarity

Surface tension is another principle of fluids at rest that we are going to analyze. Surface tension is when a liquid’s surface acts as a membrane in tension. It is caused because all the molecules of a liquid attract each other in all directions. However, the molecules on the surface attract just sideways and downward, this makes the attraction force to be bigger on the surface (see Figure 1.6). This phenomenon is responsible for the formation of droplets on the leaves of a plant and also, it allows some insects to walk over water (see Figure 1.5).

Figure 1.5 Insect walking on the surface of water

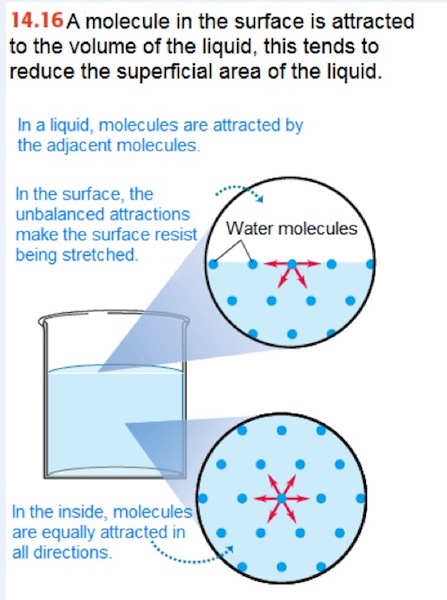
Figure 1.6 Surface tension
Source: Sears, F. and Zemansky, M. (2013). Física universitaria con física moderna (13a Ed.). México: Pearson.

The superficial tension makes hard for water to pass through small cracks or very tight conduits; to reduce it; soap or hot water can be used.

Surface tension is responsible for another phenomenon called capillarity. Capillarity  is the fluid’s capacity to go up through a capillary tube (of a very small diameter).

On a liquid, if its molecules have more adhesion than cohesion, the liquid adheres to the container walls, this causes a capillarity elevation of the surface. On the other hand, if cohesion is greater, it will originate a capillarity decrease (see Figure 1.7).

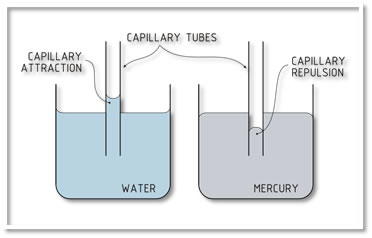
Figure 1.7 Capillary adhesion and cohesion
Source: http://chemwiki.ucdavis.edu/@api/deki/files/8632/=hg_h20_meniscus.png?revision=1

According to Burbano, Burgano and García (2003), “ascents or descents of liquids by capillary tubes, are inversely proportional to the radio of the tubes”. The formula to calculate the ascents or descents of a liquid in a capillary tube is the following:

           (1.8)

Where:

h= height reached by the liquid (m)
σ= surface tension of the liquid in contact with air (N/m)
ρ= density of the liquid (kg/m3)
r= radius of the tube (m)
g= acceleration by gravity (9.81 m/s2)

 

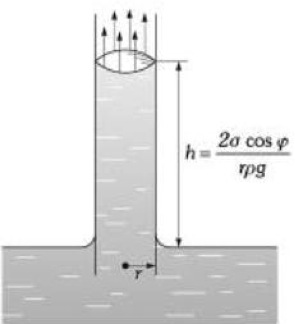
Figure 1.8 Capillarity
Source: Burbano, S., Burgano, E., y García, C. (2003). Física general (32ª ed.). España: Tébar Flores.

 

To know the value of the superficial tension of the water (σ) at different temperatures, you can access the following website.

 

---

Closure:

Go back to Figure 1.1 and explain it by using all of the principles you just learned. Why does the ice float? If the glass were narrower and taller (holding the same amount of water, ice and lemon), would the pressure at the bottom of the glass change? Would it be bigger, smaller or the same? What causes the droplets to form on the outer surface of the glass? If you insert a narrow straw, will the water on the straw rise or descend? Why?

What other practical applications can you think of? Investigate and share them with your class.

---

Bibliographic references:

• Burbano, S., Burgano, E., & García, C. (2003). Física general (32th ed.). España: Tébar Flores.
• Giaconli, D. (2005). Physics: Principles with applications (6th ed.). New Jersey, US: Pearson.
• Sears, F., & Zemansky, M. (2013). Física universitaria con física moderna (13th ed.). México: Pearson.

---